Absolute Conic-based Single View to 3D
- This project deals with single view to 3D reconstruction using classical geometric vision concepts. Here, we first design a single image-based camera intrinsics calibration module, using the concepts of Image of Absolute Conic
- Using this baseline calibration technique, we design the 3D reconstruction pipeline, using manual plane annotations
Absolute Conic and Intrinsics
Absolute Conic is an entity of the 3D projective space, \(\mathbb{P}^3\), and is represented by \(\Omega_\infty\). All spheres in \(\mathbb{P}^3\) intersect the plane at infinity, \(\pi_\infty = (0,0,0,1)^T\), at the absolute conic. It is a conic of purely imaginary points on \(\pi_\infty\). It is given as,
\[\Omega_\infty = (X_1,X_2,X_3,X_4)^T\] \[X_1^2+X_2^2+X_3^2 = 0; \hspace{0.5cm} X_4 = 0\]The image of the absolute conic (IAC), \(\omega\), is the image of the absolute conic in a camera and it relates to the intrinsics matrix as,
\[\begin{equation} \omega = (KK^T)^{-1} \end{equation}\]Camera Calibration using Vanishing Points
Here, we design a camera intrinsics calibration method, using parallel lines annotations. A triplet of parallel lines in an image has the ability to extract the matrix for the Image of Absolute Conic. This matrix can in turn be used to retrieve the camera intrinsic matrix.
Vanishing points are points where the image of two parallel lines from world space meet in the image space. Vanishing points have a property with the Image of the Absolute Conic, \(\omega\),
\[\begin{equation} \texttt{Given two vanishing points, } v_1, v_2 : \hspace{0.5cm} v_1^T \omega v_2^T =0 \end{equation}\]Using this property, if we assume that the image sensor has square pixels and zero skew, the IAC takes a form
\[\omega = \begin{bmatrix} \omega_1 & 0 & \omega_2 \\ 0 & \omega_1 & \omega_3 \\ \omega_2 & \omega_3 & \omega_4 \end{bmatrix}\]This form of IAC can be resolved using equation (2), if we have three sets of vanishing points. The intrinsics matrix, \(K\), can then be resolved by taking a cholesky decomposition of the IAC, \(\omega\), as shown in equation (1).
Using this strategy, we can resolve the intrinsics matrix, by first finding three vanishing points, by annotating three sets of parallel lines in the image, as shown in the figure below.


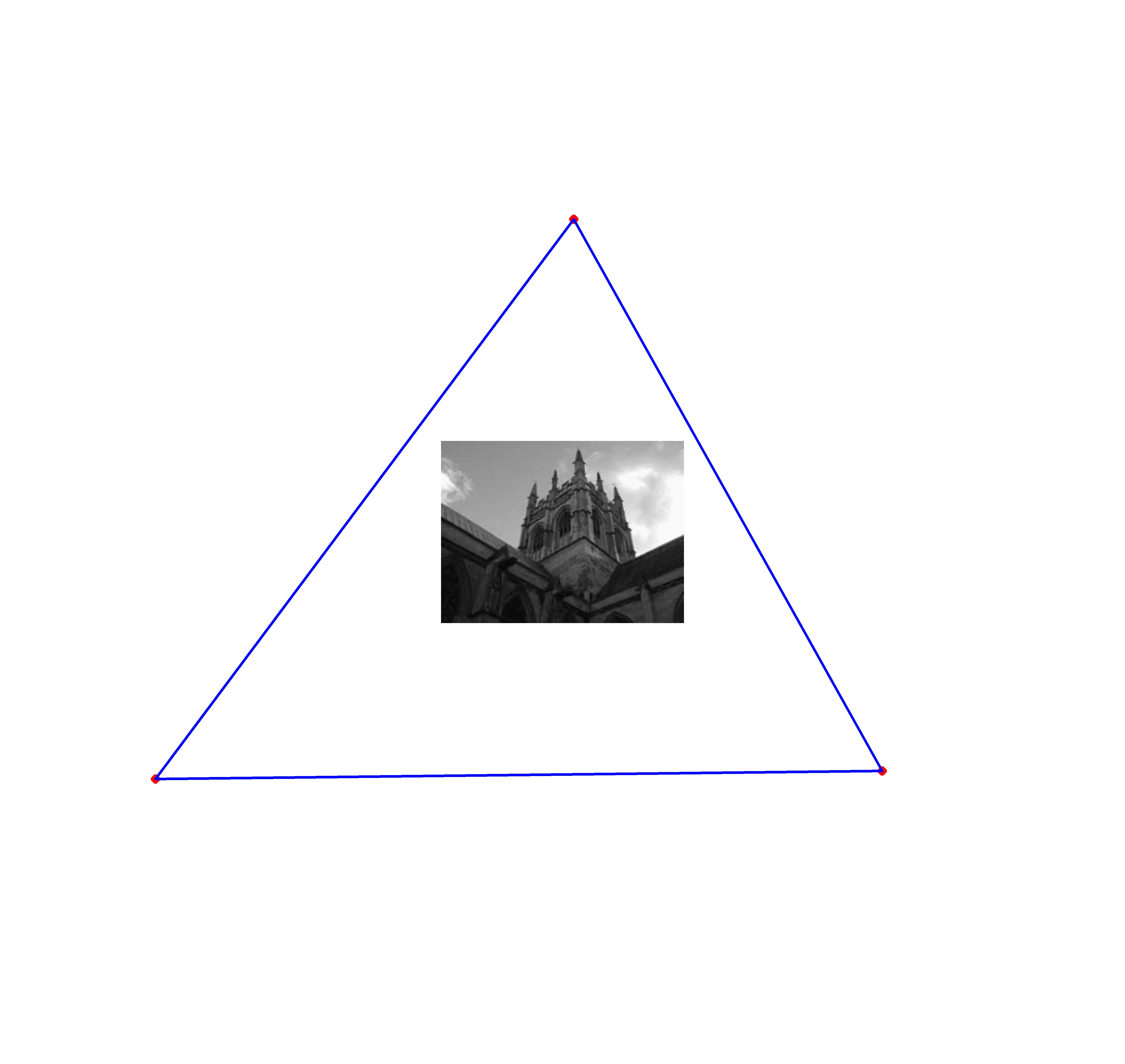
Single View Reconstruction
To perform this part, we make use of the calibration technique explained in the previous section and use that to extract the calibration matrix, \(K\). We then annotate the planes in the image, which we intend to reconstruct. The equations for these planes in \(\mathcal{R}^3\) (\(n^T X+a = 0\)) are then extracted using the \(K\) matrix and the pixels present in these planes in the image, are projected into \(\mathcal{R}^3\), using these plane equations. The results for this method can be seen below.




